[2015 arXiv] Adversarial Autoencoders

---

Table of content (short-version) [paper] [github]

• Summary
• Motivation
• Architecture
• References

---

Summary

• VAE에서 encoder가 normal distribution으로 고정된 것의 한계를 깨기 위한 방법
• GAN loss에 의해서 manifold를 N(0,1)이 아닌 다른 임의의 함수로 표현이 가능하다.

---

Motivation

• 기존 VAE의 특징
  • p와 q의 조건으로는 확률 분포로부터 샘플링을 쉽게 할 수 있어야 한다는 것과 KL 계산이 가능해야 한다는 것이다.
  • KL의 계산상의 어려움으로 encoder를 normal distribution으로 가정했었다.
  • KL term은 q가 p에 가깝게 확률분포를 변화시키는 과정
• KL 대신 GAN loss의 이용
  • VAE에서 KL의 기능은 GAN과 유사 (타겟 분포와 생성된 샘플이 있을 때, 샘플들의 분포를 타겟 분포와 같게 만드는 방식)
  • 즉, KL대신 GAN loss를 사용하면 임의의 함수에 대해서도 샘플링을 한 뒤 GAN의 개념을 적용함으로써 KL계산 없이 AE수행을 가능하게 함
  • 따라서 모델 선팩의 폭이 넓어진다.

---

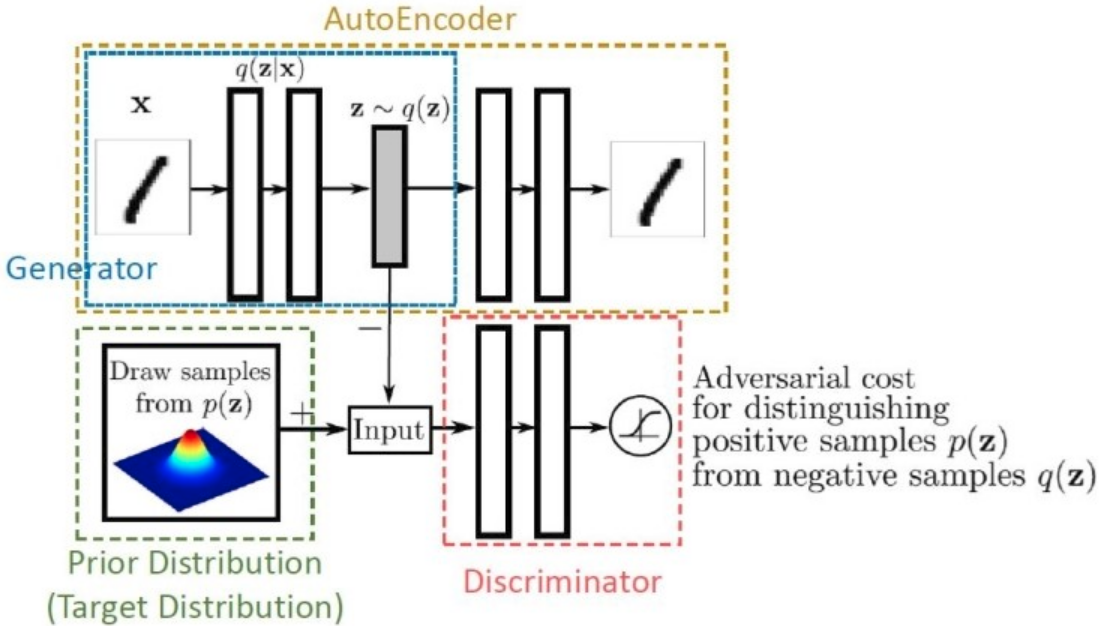
Architecture

• Loss
  • 학습1(update AE $\rightarrow$ $\phi, \theta$): $L_i(\phi, \theta, x_i) = - \mathbb{E}_{q_\phi (z|x_i)} [log(p_\theta (x_i|z))]$
  • 학습2(update D $\rightarrow$ $\lambda$): $-V_i(\phi, \lambda, x_i, z_i) = - log(d_\lambda (z_i))-log(1-d_\lambda (q_\phi (x_i)))$
  • 학습3(update G $\rightarrow$ $\phi$): $-V_i(\phi, \lambda, x_i, z_i) = - log(d_\lambda (q_\phi (x_i)))$
• Discriminator는 p(z)로부터의 샘플을 pos로, q(z)를 neg로 구분
• Manifold 모양을 볼 때 VAE는 자주 나오는 값을 중시하여 빈 공간이 가끔 있지만, AAE는 분포의 모양을 중시하여 빈공간이 적다.
• 기존 VAE에 비해서 image-level 분포가 아닌 latent-space 분포를 같게 한다는게 핵심 아이디어

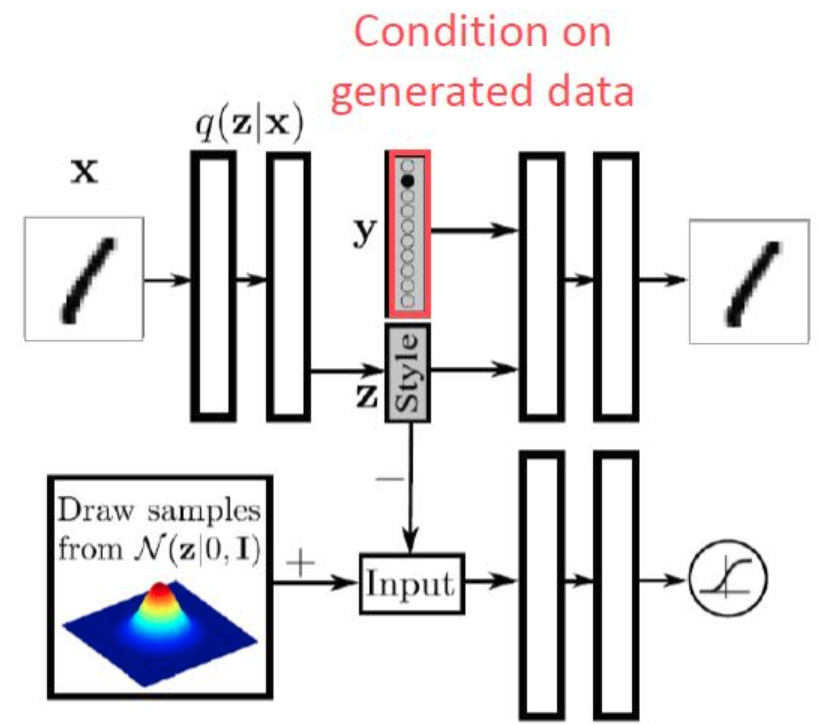
[기본 VAE에서 conditional 추가된 버전 (Supervised)]

[Supervised AAE]

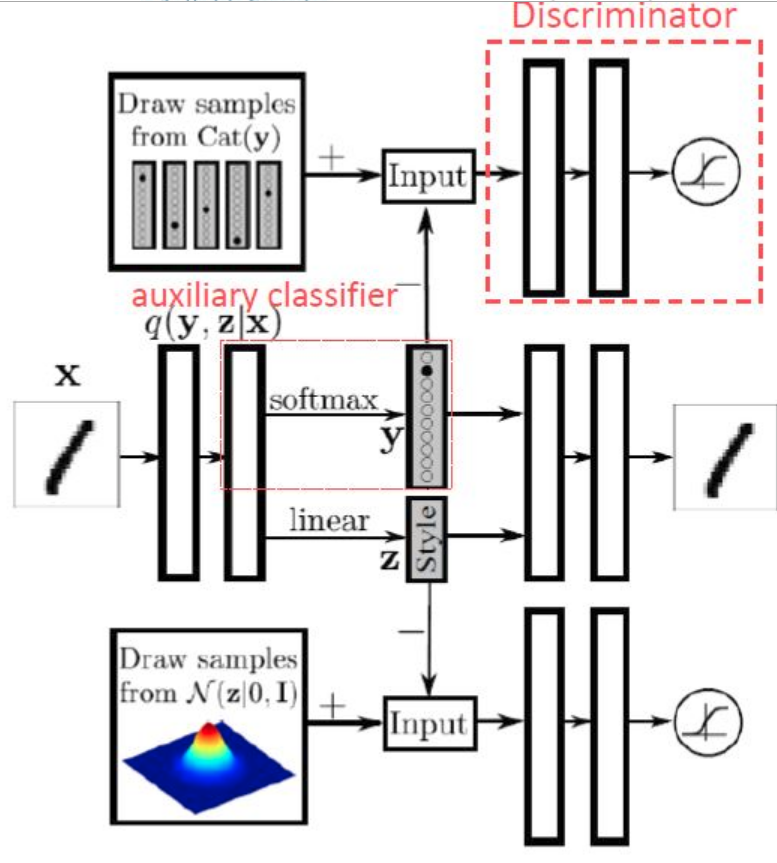
[Semi-supervised AAE (auxiliary classifier)]

---

References

[1] Makhzani, Alireza, et al. “Adversarial autoencoders.” arXiv preprint arXiv:1511.05644 (2015).

[2] https://ratsgo.github.io/generative%20model/2018/01/28/VAEs/

[3] https://rubikscode.net/2019/01/14/introduction-to-adversarial-autoencoders/

[4] https://www.inference.vc/adversarial-autoencoders/

[5] https://hjweide.github.io/adversarial-autoencoders

[6] https://blog.naver.com/stykworld/221378497228